3d integral for finding temperature distribution in a box Again, since the l.h.s. depends only on r and the r.h.s. on θ, both must be equal to a constant μ, See more APX Incorporated is comprised of five fully integrated manufacturing operations. In addition to APX Enclosures (NEMA Enclosures & ITS Enclosures) the APX Company is comprised of .
0 · heat source temperature distribution
1 · 3d heat equation
Other Videos:How make a night lamp: https://youtu.be/sP-RsSL53MoHello Viewers. in this video i will be showing how to use Easel platform to engrave on CNC 30.
where A is any function that is smooth (i.e. continuously differentiable) for x ∈ V . Note that � ∂ ∂ ∂ ∂ See more
We now consider the special case where the subregion D is a rectangle See more+ ˆey + ˆez ∂y ∂z where ˆex, ˆey, ˆez are the unit vectors in the x, y, z directions, respectively. The divergence of a vector valued function F = (Fx, Fy, Fz) is See moreAgain, since the l.h.s. depends only on r and the r.h.s. on θ, both must be equal to a constant μ, See more
This manuscript presents a heat transfer model for predicting the three-dimensional temperature field in a multi-die 3D IC with unequally-sized die. This problem is solved .
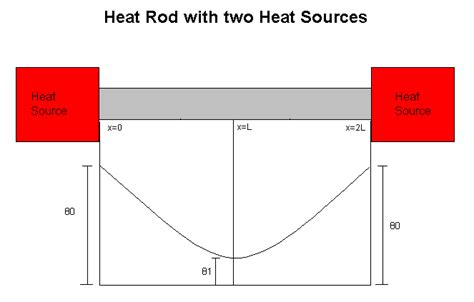
It will come as no surprise that we can also do triple integrals—integrals over a three-dimensional region. The simplest application allows us to compute volumes in an alternate way. To .These situations can be analyzed by looking at a model problem of a slab with heat sources (W/m 3) distributed throughout. We take the outside walls to be at temperature and we will determine the maximum internal temperature. or .A metal bar with length L= ˇis initially heated to a temperature of u 0(x). The temper-ature distribution in the bar is u(x;t). At the ends, it is exposed to air; the temperature outside is .
temperature distribution(the variation of temperature) throughout the medium in order to calculate some quantities of interest such as the local heat transfer rate, thermal expansion, and thermal .In convection heat transfer, the heat is moved through bulk transfer of a non-uniform temperature fluid. The third process is radiation or transmission of energy through space without the .
Find the average temperature in the box D={(x,y,z): 0<=x<=Ln(2), 0<=y<=Ln(4), 0<=z<=Ln(8)} with a temperature distribution of T(x,y,z)=128e^(-x-y-z). In your answer please show the triple .
1. A bar with initial temperature profile f (x) > 0, with ends held at 0o C, will cool as t → ∞, and approach a steady-state temperature 0o C. However, whether or not all parts of the bar start .application of boundary conditions is simpler. [This is an example of finding a general principle and then trying to find a way to violate it.] ψ(x) = A. sin . kx + B. cos. kx . Apply boundary .Consider an arbitrary 3D subregion V of R3 (V ⊆ R3), with temperature u(x,t) defined at all points x = (x,y,z) ∈ V. We generalize the ideas of 1-D heat flux to This manuscript presents a heat transfer model for predicting the three-dimensional temperature field in a multi-die 3D IC with unequally-sized die. This problem is solved iteratively using solutions of three simpler heat transfer problems outlined in the manuscript.
It will come as no surprise that we can also do triple integrals—integrals over a three-dimensional region. The simplest application allows us to compute volumes in an alternate way. To approximate a volume in three dimensions, we can divide the three-dimensional region into small rectangular boxes, each $\Delta x\times\Delta y\times\Delta z .
heat source temperature distribution
These situations can be analyzed by looking at a model problem of a slab with heat sources (W/m 3) distributed throughout. We take the outside walls to be at temperature and we will determine the maximum internal temperature. or There is a change in heat flux with due to the presence of the heat sources. The equation for the temperature is. (18..
A metal bar with length L= ˇis initially heated to a temperature of u 0(x). The temper-ature distribution in the bar is u(x;t). At the ends, it is exposed to air; the temperature outside is constant, so we require that u= 0 at the endpoints of the bar. Over time, we expect the heat to di use or be lost to the environment until the temperaturetemperature distribution(the variation of temperature) throughout the medium in order to calculate some quantities of interest such as the local heat transfer rate, thermal expansion, and thermal stress at some critical locations at speci-fied times. The specification of the temperature at a point in a medium first re-In convection heat transfer, the heat is moved through bulk transfer of a non-uniform temperature fluid. The third process is radiation or transmission of energy through space without the necessary presence of matter. Radiation is the only method for heat transfer in space.
Find the average temperature in the box D={(x,y,z): 0<=x<=Ln(2), 0<=y<=Ln(4), 0<=z<=Ln(8)} with a temperature distribution of T(x,y,z)=128e^(-x-y-z). In your answer please show the triple integral you set up as well as how you determined the limits of integration.
1. A bar with initial temperature profile f (x) > 0, with ends held at 0o C, will cool as t → ∞, and approach a steady-state temperature 0o C. However, whether or not all parts of the bar start cooling initially depends on the shape of the initial temperature profile.application of boundary conditions is simpler. [This is an example of finding a general principle and then trying to find a way to violate it.] ψ(x) = A. sin . kx + B. cos. kx . Apply boundary conditions ψ(0) =0 =0 + B . →. B =0 . n. π. ψ(a) =0 = A. sin . ka . ⇒. ka = n. π, k. n = a . ∞. a ⎛ Normalize: 1 = ∫. −∞. dx. ψ*ψ= A .Consider an arbitrary 3D subregion V of R3 (V ⊆ R3), with temperature u(x,t) defined at all points x = (x,y,z) ∈ V. We generalize the ideas of 1-D heat flux to This manuscript presents a heat transfer model for predicting the three-dimensional temperature field in a multi-die 3D IC with unequally-sized die. This problem is solved iteratively using solutions of three simpler heat transfer problems outlined in the manuscript.
It will come as no surprise that we can also do triple integrals—integrals over a three-dimensional region. The simplest application allows us to compute volumes in an alternate way. To approximate a volume in three dimensions, we can divide the three-dimensional region into small rectangular boxes, each $\Delta x\times\Delta y\times\Delta z .These situations can be analyzed by looking at a model problem of a slab with heat sources (W/m 3) distributed throughout. We take the outside walls to be at temperature and we will determine the maximum internal temperature. or There is a change in heat flux with due to the presence of the heat sources. The equation for the temperature is. (18..A metal bar with length L= ˇis initially heated to a temperature of u 0(x). The temper-ature distribution in the bar is u(x;t). At the ends, it is exposed to air; the temperature outside is constant, so we require that u= 0 at the endpoints of the bar. Over time, we expect the heat to di use or be lost to the environment until the temperature
temperature distribution(the variation of temperature) throughout the medium in order to calculate some quantities of interest such as the local heat transfer rate, thermal expansion, and thermal stress at some critical locations at speci-fied times. The specification of the temperature at a point in a medium first re-In convection heat transfer, the heat is moved through bulk transfer of a non-uniform temperature fluid. The third process is radiation or transmission of energy through space without the necessary presence of matter. Radiation is the only method for heat transfer in space.Find the average temperature in the box D={(x,y,z): 0<=x<=Ln(2), 0<=y<=Ln(4), 0<=z<=Ln(8)} with a temperature distribution of T(x,y,z)=128e^(-x-y-z). In your answer please show the triple integral you set up as well as how you determined the limits of integration.1. A bar with initial temperature profile f (x) > 0, with ends held at 0o C, will cool as t → ∞, and approach a steady-state temperature 0o C. However, whether or not all parts of the bar start cooling initially depends on the shape of the initial temperature profile.
3d heat equation
$19.16
3d integral for finding temperature distribution in a box|heat source temperature distribution