black box distribution planck Planck's law describes the unique and characteristic spectral distribution for electromagnetic radiation in thermodynamic equilibrium, when there is no net flow of matter . See more $6.59
0 · The Derivation of the Planck Formula
1 · Planck’s radiation law
2 · Planck’s Derivation of the Energy Density of Blackbody
3 · Planck's law
4 · Blackbody Radiation
5 · Black Body Radiation
6 · Black
7 · 6.2: Blackbody Radiation
8 · 13 Black
Yes, the BOX will hold at least 20 pounds. When the sheetrock fails, the box will still be securely fastened to the fixture as it falls on your head. The substrate doesn't just need to hold the fixture weight.
In physics, Planck's law (also Planck radiation law ) describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment. At the end of the 19th century, physicists were . See moreEvery physical body spontaneously and continuously emits electromagnetic radiation and the spectral radiance of a body, Bν, describes the spectral emissive power per unit area, . See more
Planck's law can be encountered in several forms depending on the conventions and preferences of different scientific fields. The . See morePlanck's law describes the unique and characteristic spectral distribution for electromagnetic radiation in thermodynamic equilibrium, when there is no net flow of matter . See moreBalfour StewartIn 1858, Balfour Stewart described his experiments on the thermal radiative emissive and absorptive powers of polished plates of . See moreA black-body is an idealised object which absorbs and emits all radiation frequencies. Near thermodynamic equilibrium, the emitted radiation is closely described by Planck's law and because of its dependence on temperature, Planck radiation is said to . See more
PeaksThe distributions Bν, Bω, Bν̃ and Bk peak at a photon energy of See more
Photon gasConsider a cube of side L with conducting walls filled with electromagnetic radiation in thermal equilibrium at temperature T. If there is a small hole in one of the walls, the radiation emitted from the hole will be characteristic of a . See more
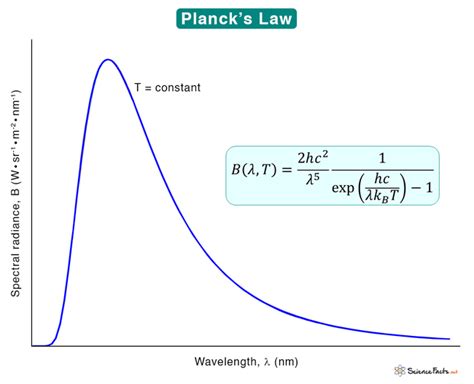
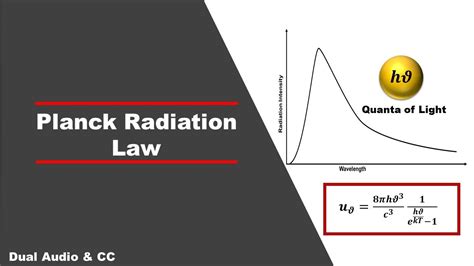
Black-body radiation has a characteristic, continuous frequency spectrum that depends only on the body's temperature, called the Planck spectrum or Planck's law. The spectrum is peaked at a characteristic frequency that shifts to higher frequencies with increasing temperature, and at room temperature most of the emission is in the infrared region of the electromagnetic spectrum. As the temp.The blackbody radiation problem was solved in 1900 by Max Planck. Planck used the same idea as the Rayleigh–Jeans model in the sense that he treated the electromagnetic waves between the walls inside the cavity classically, and .The first successful theoretical analysis of the data was by Max Planck in 1900. He concentrated on modeling the oscillating charges that must exist in the oven walls, radiating heat inwards and — in thermodynamic equilibrium — .
This now famous equation is known as the Planck Distribution Law for Blackbody Radiation.The h in this equation is the famous Planck’s constant, which has a value of \(6.626 \times 10^-34\; J \;s\).K (T) = E |black body: Thus, the meaning of the universal (i.e., material- and shape-independent) constant K (T) is that it is the density of radiation (per wavelength interval) emitted by a black .
Planck’s radiation law, a mathematical relationship formulated in 1900 by German physicist Max Planck to explain the spectral-energy distribution of radiation emitted by a blackbody (a hypothetical body that absorbs all radiant energy .
Planck’s Derivation of the Energy Density of Blackbody Radiation To calculate the number of modes of oscillation of electromagnetic radiation possible in a cavity, consider a one .Black-Body Radiation Goal: Test Planck’s law and the Stephan-Boltzmann law Equipment: Tungsten lamp with power supply, Ocean Optics spectrometer, pyrometer 1. Introduction The .
In physics, Planck's law (also Planck radiation law [1]: 1305 ) describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.Black-body radiation is the thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body (an idealized opaque, non-reflective body).
The blackbody radiation problem was solved in 1900 by Max Planck. Planck used the same idea as the Rayleigh–Jeans model in the sense that he treated the electromagnetic waves between the walls inside the cavity classically, and assumed that .The first successful theoretical analysis of the data was by Max Planck in 1900. He concentrated on modeling the oscillating charges that must exist in the oven walls, radiating heat inwards and — in thermodynamic equilibrium — themselves being driven by the radiation field.
The Derivation of the Planck Formula
the Planck Formula Topics The Planck formula for black-body radiation. Revision of waves in a box. Radiation in thermal equilibrium. The equipartition theorem and the ultraviolet catastrophe. The photoelectric efiect. The wave-particle duality. Quantisation of radiation and the derivation of the Planck spectrum. The Stefan-Boltzmann law. 10.1 . This now famous equation is known as the Planck Distribution Law for Blackbody Radiation.The h in this equation is the famous Planck’s constant, which has a value of \(6.626 \times 10^-34\; J \;s\).K (T) = E |black body: Thus, the meaning of the universal (i.e., material- and shape-independent) constant K (T) is that it is the density of radiation (per wavelength interval) emitted by a black body. Incidentally, since the absorption by a black body is the maximum and the ratio of the emitted to absorbed amounts of radi-Planck’s radiation law, a mathematical relationship formulated in 1900 by German physicist Max Planck to explain the spectral-energy distribution of radiation emitted by a blackbody (a hypothetical body that absorbs all radiant energy falling upon it).
Planck’s Derivation of the Energy Density of Blackbody Radiation To calculate the number of modes of oscillation of electromagnetic radiation possible in a cavity, consider a one-dimensional box of side L. In equilibrium only standing waves are possible, and these will have nodes at the ends x = 0, L. L x= n 2 nx = 1, 2,Black-Body Radiation Goal: Test Planck’s law and the Stephan-Boltzmann law Equipment: Tungsten lamp with power supply, Ocean Optics spectrometer, pyrometer 1. Introduction The Planck distribution law states that a “black” body at temperature T emits radiation with a spectral distribution f(λ) given by ( , ) 1 8 ( ) 5 T e hc f k T h c .In physics, Planck's law (also Planck radiation law [1]: 1305 ) describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.Black-body radiation is the thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body (an idealized opaque, non-reflective body).
The blackbody radiation problem was solved in 1900 by Max Planck. Planck used the same idea as the Rayleigh–Jeans model in the sense that he treated the electromagnetic waves between the walls inside the cavity classically, and assumed that .The first successful theoretical analysis of the data was by Max Planck in 1900. He concentrated on modeling the oscillating charges that must exist in the oven walls, radiating heat inwards and — in thermodynamic equilibrium — themselves being driven by the radiation field.the Planck Formula Topics The Planck formula for black-body radiation. Revision of waves in a box. Radiation in thermal equilibrium. The equipartition theorem and the ultraviolet catastrophe. The photoelectric efiect. The wave-particle duality. Quantisation of radiation and the derivation of the Planck spectrum. The Stefan-Boltzmann law. 10.1 .
metal post to wood fence bracket canada
This now famous equation is known as the Planck Distribution Law for Blackbody Radiation.The h in this equation is the famous Planck’s constant, which has a value of \(6.626 \times 10^-34\; J \;s\).K (T) = E |black body: Thus, the meaning of the universal (i.e., material- and shape-independent) constant K (T) is that it is the density of radiation (per wavelength interval) emitted by a black body. Incidentally, since the absorption by a black body is the maximum and the ratio of the emitted to absorbed amounts of radi-Planck’s radiation law, a mathematical relationship formulated in 1900 by German physicist Max Planck to explain the spectral-energy distribution of radiation emitted by a blackbody (a hypothetical body that absorbs all radiant energy falling upon it).
Planck’s Derivation of the Energy Density of Blackbody Radiation To calculate the number of modes of oscillation of electromagnetic radiation possible in a cavity, consider a one-dimensional box of side L. In equilibrium only standing waves are possible, and these will have nodes at the ends x = 0, L. L x= n 2 nx = 1, 2,
metal pump enclosure
Find Bracket shelf wall mounted shelving at Lowe's today. Shop wall mounted shelving and a variety of storage & organization products online at Lowes.com.
black box distribution planck|Planck’s Derivation of the Energy Density of Blackbody