box muller distribution • Inverse transform sampling• Marsaglia polar method, similar transform to Box–Muller, which uses Cartesian coordinates, instead of polar coordinates See more Get the best deals for Western Electric Phone Wood at eBay.com. We have a great online selection at the lowest prices with Fast & Free shipping on many items!
0 · proof of box muller
1 · how to calculate box muller
2 · box muller wikipedia
3 · box muller transformation
4 · box muller method formula
5 · box muller maths
6 · box muller generator
7 · box muller formula
Stick welding sheet metal can be done by welding DC electrode negative with 20-40A which is about the the lowest amperage settings that still allows to strike an arc. Suitable electrodes are E6011 for rusty or painted surfaces or E6013 for clean surfaces.
The Box–Muller transform, by George Edward Pelham Box and Mervin Edgar Muller, is a random number sampling method for generating pairs of independent, standard, normally distributed (zero expectation, unit variance) random numbers, given a source of uniformly distributed random numbers. The method . See more

Suppose U1 and U2 are independent samples chosen from the uniform distribution on the unit interval (0, 1). Let See moreThe polar method differs from the basic method in that it is a type of rejection sampling. It discards some generated random numbers, but can be faster than the basic method . See more• Inverse transform sampling• Marsaglia polar method, similar transform to Box–Muller, which uses Cartesian coordinates, instead of polar coordinates See more• Weisstein, Eric W. "Box-Muller Transformation". MathWorld.• How to Convert a Uniform Distribution to a Gaussian Distribution (C Code) See more
The polar form was first proposed by J. Bell and then modified by R. Knop. While several different versions of the polar method have been described, the version of R. Knop will be . See moreC++The standard Box–Muller transform generates values from the standard normal distribution (i.e. standard normal deviates) with mean 0 and standard deviation 1. The implementation below in standard See more
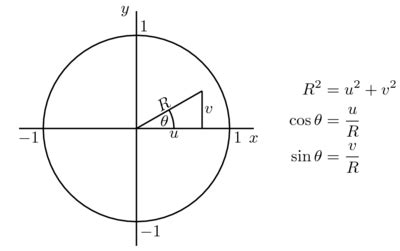
A transformation which transforms from a two-dimensional continuous uniform distribution to a two-dimensional bivariate normal distribution (or complex normal distribution). Exercise (Box–Muller method): Let $U$ and $V$ be independent random variables that are uniformly distributed on $[0,1]$. Define $$X := \sqrt{−2\log(U)}\, \cos(2\pi V) \quad .
Two simple ways to simulate a pair of independent standard normal distributions. The Box–Muller transform is a pseudo-random number sampling method for generating pairs of independent, standard, normally .
1 Box Muller It would be nice to get a standard normal from a standard uniform by inverting the distribution function, but there is no closed form formula for this distribution function N(x) = P(X . A Box–Muller transform (by George Edward Pelham Box and Mervin Edgar Muller 1958) [1] is a method of generating pairs of independent standard normally distributed (zero . For this project, my goal is to generate Gaussian samples in two dimensions i.e. generating samples whose x and y coordinates are independent standard normals (Gaussian with zero mean and standard.
The Box-Muller Transformation takes two uniformly distributed random numbers and transforms them into two normally distributed random numbers. The transformation is based on the fact . Here’s the Box-Muller method for simulating two (independent) standard normal variables with two (independent) uniform random variables. Two (independent) standard .The Box–Muller transform, by George Edward Pelham Box and Mervin Edgar Muller, [1] is a random number sampling method for generating pairs of independent, standard, normally distributed (zero expectation, unit variance) random numbers, given a source of uniformly distributed random numbers. A transformation which transforms from a two-dimensional continuous uniform distribution to a two-dimensional bivariate normal distribution (or complex normal distribution).
Exercise (Box–Muller method): Let $U$ and $V$ be independent random variables that are uniformly distributed on $[0,1]$. Define $$X := \sqrt{−2\log(U)}\, \cos(2\pi V) \quad \text{and} \quad Y := \sqrt{−2\log(U)}\, \sin(2\pi V)\, .$$ Two simple ways to simulate a pair of independent standard normal distributions. The Box–Muller transform is a pseudo-random number sampling method for generating pairs of independent, standard, normally distributed (zero expectation, unit variance) random numbers, given a source of uniformly distributed random numbers.A Box Muller transform takes a continuous, two dimensional uniform distribution and transforms it to a normal distribution. It is widely used in statistical sampling, and is an easy to run, elegant way to come up with a standard normal model.1 Box Muller It would be nice to get a standard normal from a standard uniform by inverting the distribution function, but there is no closed form formula for this distribution function N(x) = P(X < x) = √1 2π R x −∞ e−x02/2dx0. The Box Muller method is a brilliant trick to overcome this by producing two independent standard normals
A Box–Muller transform (by George Edward Pelham Box and Mervin Edgar Muller 1958) [1] is a method of generating pairs of independent standard normally distributed (zero expectation, unit variance) random numbers, given a source of . For this project, my goal is to generate Gaussian samples in two dimensions i.e. generating samples whose x and y coordinates are independent standard normals (Gaussian with zero mean and standard.
The Box-Muller Transformation takes two uniformly distributed random numbers and transforms them into two normally distributed random numbers. The transformation is based on the fact that the sum of two independent uniformly distributed random variables has a normal distribution. Here’s the Box-Muller method for simulating two (independent) standard normal variables with two (independent) uniform random variables. Two (independent) standard normal random variable Z1 and Z2. Generate two (independent) uniform random variables U1 ∼ U(0, 1) and U2 ∼ U(0, 1).The Box–Muller transform, by George Edward Pelham Box and Mervin Edgar Muller, [1] is a random number sampling method for generating pairs of independent, standard, normally distributed (zero expectation, unit variance) random numbers, given a source of uniformly distributed random numbers. A transformation which transforms from a two-dimensional continuous uniform distribution to a two-dimensional bivariate normal distribution (or complex normal distribution).

Exercise (Box–Muller method): Let $U$ and $V$ be independent random variables that are uniformly distributed on $[0,1]$. Define $$X := \sqrt{−2\log(U)}\, \cos(2\pi V) \quad \text{and} \quad Y := \sqrt{−2\log(U)}\, \sin(2\pi V)\, .$$
proof of box muller
Two simple ways to simulate a pair of independent standard normal distributions. The Box–Muller transform is a pseudo-random number sampling method for generating pairs of independent, standard, normally distributed (zero expectation, unit variance) random numbers, given a source of uniformly distributed random numbers.A Box Muller transform takes a continuous, two dimensional uniform distribution and transforms it to a normal distribution. It is widely used in statistical sampling, and is an easy to run, elegant way to come up with a standard normal model.
1 Box Muller It would be nice to get a standard normal from a standard uniform by inverting the distribution function, but there is no closed form formula for this distribution function N(x) = P(X < x) = √1 2π R x −∞ e−x02/2dx0. The Box Muller method is a brilliant trick to overcome this by producing two independent standard normals A Box–Muller transform (by George Edward Pelham Box and Mervin Edgar Muller 1958) [1] is a method of generating pairs of independent standard normally distributed (zero expectation, unit variance) random numbers, given a source of . For this project, my goal is to generate Gaussian samples in two dimensions i.e. generating samples whose x and y coordinates are independent standard normals (Gaussian with zero mean and standard.
The Box-Muller Transformation takes two uniformly distributed random numbers and transforms them into two normally distributed random numbers. The transformation is based on the fact that the sum of two independent uniformly distributed random variables has a normal distribution.
ethernet cat5e junction box

Metals Depot - America's Metal Superstore is your complete supplier for industrial metals worldwide. Stocking over 50,000 Shapes, Sizes, Types and Lengths of Steel, Aluminum, Stainless, Brass, Copper, Cold Finish Steel, Tool Steel and Alloy Steels among our network of warehouses, at Wholesale Prices.
box muller distribution|box muller method formula